 |
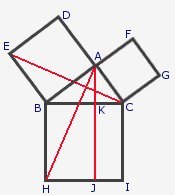 |
The Theorem ABC is a right angled triangle The area of the square on the hypotenuse BC is equal to the sum of the squares on the other two sides. The Proof Construct the squares ABED, ACGF and BCIH on the sides AB, AC and BC respectively. Construct the lines EC and AH Draw AJ the perpendicular from A to side HI. Consider the two triangles EBC , ABH. BC = BH Angle EBC = Angle ABH (right angle + Angle ABC) Therefore, the triangles are congruent (Side/Angle/Side) Therefore, the triangles are equal in area. The area of the triangle EBC is half the area of the square EBAD (same base EB and same height) The area of the triangle ABH is half the area of the square BKJH (same base BH and same height) Therefore, Area EBAD = Area BKJH Similarly, Area ACGF = Area KCIJ Therefore, Area EBAD + Area ACGF = Area BKJH + Area KCIJ = Area BCIH |